Contoh Kurva Lorenz dan Gini Ratio yang Ekstrem
Kurva Lorenz merupakan indikator sederhana untuk menunjukkan kondisi pembagian pendapatan (atau kekayaan) di satu daerah. Kurva Lorenz menggambarkan kumulatif pendapatan yang diterima oleh kumulatif penduduk di satu daerah tertentu.
Pada pembagian pendapatan yang merata, 10 persen penduduk termiskin mendapat 10 persen pendapatan terendah. Kemudian, 20 persen penduduk termiskin mendapat 20 persen pendapatan terendah. Seterusnya, 30 persen penduduk termiskin mendapatkan 30 persen pendapatan terendah. Dan seterusnya.
Karena setiap akumulasi penduduk mendapat pendapatan sesuai dengan proporsinya, maka setiap pendapatan akan dibagi secara merata.
Jika dibentuk sebuah kurva, akan terbentuk kurva seperti gambar 1.
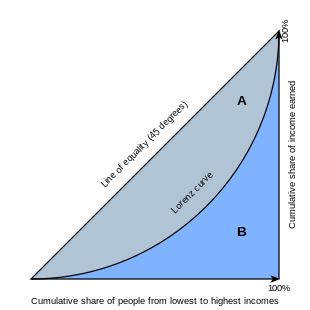
Pada gambar di atas, kurva diagonal menggambarkan kondisi distribusi pendapatan yang merata. Kurva Lorenz berada di bawah kurva diagonal, berarti ada kondisi pembagian pendapatan yang tidak merata.
Semakin jauh kurva Lorenz dari kurva diagonal, maka kondisi distribusi dikatakan semakin tidak merata. Sebaliknya, jika kurva Lorenz semakin mendekati diagonal, maka kondisi distribusi dikatakan semakin merata.
Menghitung Gini Ratio dari Kurva Lorenz
Perbandingan kondisi ketidakmerataan dapat menggunakan kurva Lorenz membawa kendala bagi peneliti yang ingin membandingkan dua Kurva Lorenz yang hampir mirip satu sama lain.
Oleh karena itu, diperlukan satu indikator yang lebih sederhana untuk dapat menunjukkan kondisi ketimpangan, yakni Gini Ratio. Gini Ratio merupakan satu angka tunggal yang menunjukkan kondisi ketimpangan. Gini Ratio memiliki nilai antara nol dan satu. Gini Ratio nol berarti kondisi distribusi merata, dan Gini ratio satu berarti kondisi paling tidak merata.
Berdasarkan gambar di atas, Gini Ratio didapat dari rasio antara luas wilayah antara kurva Lorenz dan kurva diagonal (yakni wilayah A) dengan luas seluruh wilayah yang berada di bawah kurva diagonal (yakni wilayah A+B). Luas A+B sama dengan luas segitiga.
Maka Gini Ratio adalah A/(A+B)
Pada gambar di atas, panjang sumbu yang membentuk segitiga adalah 100% (=1) maka luas segitiga adalah 0.5. Dengan demikian, luas A+B=0,5.
Jika luas A diasumsikan setengah dari luas A+B, maka luas A adalah 0.25.
Maka, Gini Ratio adalah A/(A+B)=0,25/0,5=0,5
Gini Ratio dan Kurva Lorenz yang Ekstrem
Pada Kurva Lorenz, sumbu horizontal menunjukkan akumulasi populasi, sehingga nilainya tidak pernah negatif (karena populasi tidak pernah negatif). Sementara sumbu vertikal menunjukkan nilai yang didistribusikan kepada populasi, bisa berupa pendapatan, pengeluaran, atau kekayaan.
Kurva Lorenz yang ekstrem ditandai dengan posisi kurva yang menyentuh nilai negatif pada sumbu vertikal (Gambar 2).
Pada Gambar 2, sumbu vertikal menunjukkan akumulasi kekayaan, sementara sumbu horizontal menunjukkan akumulasi populasi.
Bagian yang diarsir (A+C) menunjukkan area Gini Ratio. Jika ada satu bagian kurva Lorenz yang berada di bawah sumbu horizontal maka secara teoretis, nilai Gini Ratio bisa bernilai lebih besar dari satu .
Contohnya adalah perhitungan kekayaan bersih di Indonesia. Kekayaan bersih bisa bernilai negatif, yakni jika nilai seluruh harta (kekayaan) lebih kecil daripada hutang. Pada Kurva Lorenz, saat ada banyak masyarakat yang memiliki kekayaan bersih negatif maka akan membuat Kurva Lorenz memiliki sumbu vertikal yang negatif (Gambar 3).

Pengamatan atas ketiga kurva di Gambar 3 menunjukkan kondisi distribusi yang paling buruk adalah pada tahun 1997 (tengah) dimana Kurva Lorens memiliki posisi paling jauh dari kurva horizontal dan bernilai negatif. Kemudian, kondisi distribusi paling baik adalah pada tahun 2000 (kanan), dimana posisi kurva pada tahun ini paling mendekati garis diagonal.
Dengan perhitungan matematis, Gini Ratio pada tahun 1993 (kiri) adalah 0.897 dan untuk tahun 1997 (tengah) adalah 1,092. Sementara Gini Ratio untuk tahun 2000 adalah 0,690.
(Thomas Soseco)
Artikel Terkait:
Pada pembagian pendapatan yang merata, 10 persen penduduk termiskin mendapat 10 persen pendapatan terendah. Kemudian, 20 persen penduduk termiskin mendapat 20 persen pendapatan terendah. Seterusnya, 30 persen penduduk termiskin mendapatkan 30 persen pendapatan terendah. Dan seterusnya.
Karena setiap akumulasi penduduk mendapat pendapatan sesuai dengan proporsinya, maka setiap pendapatan akan dibagi secara merata.
Jika dibentuk sebuah kurva, akan terbentuk kurva seperti gambar 1.

Gambar 1. Kurva Lorenz (Sumber: Wikipedia)
Pada gambar di atas, kurva diagonal menggambarkan kondisi distribusi pendapatan yang merata. Kurva Lorenz berada di bawah kurva diagonal, berarti ada kondisi pembagian pendapatan yang tidak merata.
Semakin jauh kurva Lorenz dari kurva diagonal, maka kondisi distribusi dikatakan semakin tidak merata. Sebaliknya, jika kurva Lorenz semakin mendekati diagonal, maka kondisi distribusi dikatakan semakin merata.
Menghitung Gini Ratio dari Kurva Lorenz
Perbandingan kondisi ketidakmerataan dapat menggunakan kurva Lorenz membawa kendala bagi peneliti yang ingin membandingkan dua Kurva Lorenz yang hampir mirip satu sama lain.
Oleh karena itu, diperlukan satu indikator yang lebih sederhana untuk dapat menunjukkan kondisi ketimpangan, yakni Gini Ratio. Gini Ratio merupakan satu angka tunggal yang menunjukkan kondisi ketimpangan. Gini Ratio memiliki nilai antara nol dan satu. Gini Ratio nol berarti kondisi distribusi merata, dan Gini ratio satu berarti kondisi paling tidak merata.
Berdasarkan gambar di atas, Gini Ratio didapat dari rasio antara luas wilayah antara kurva Lorenz dan kurva diagonal (yakni wilayah A) dengan luas seluruh wilayah yang berada di bawah kurva diagonal (yakni wilayah A+B). Luas A+B sama dengan luas segitiga.
Maka Gini Ratio adalah A/(A+B)
Pada gambar di atas, panjang sumbu yang membentuk segitiga adalah 100% (=1) maka luas segitiga adalah 0.5. Dengan demikian, luas A+B=0,5.
Jika luas A diasumsikan setengah dari luas A+B, maka luas A adalah 0.25.
Maka, Gini Ratio adalah A/(A+B)=0,25/0,5=0,5
Gini Ratio dan Kurva Lorenz yang Ekstrem
Pada Kurva Lorenz, sumbu horizontal menunjukkan akumulasi populasi, sehingga nilainya tidak pernah negatif (karena populasi tidak pernah negatif). Sementara sumbu vertikal menunjukkan nilai yang didistribusikan kepada populasi, bisa berupa pendapatan, pengeluaran, atau kekayaan.
Kurva Lorenz yang ekstrem ditandai dengan posisi kurva yang menyentuh nilai negatif pada sumbu vertikal (Gambar 2).
Gambar 2. Kurva Lorenz yang ekstrim (Sumber: Dagum, 1999)
Pada Gambar 2, sumbu vertikal menunjukkan akumulasi kekayaan, sementara sumbu horizontal menunjukkan akumulasi populasi.
Bagian yang diarsir (A+C) menunjukkan area Gini Ratio. Jika ada satu bagian kurva Lorenz yang berada di bawah sumbu horizontal maka secara teoretis, nilai Gini Ratio bisa bernilai lebih besar dari satu .
Contohnya adalah perhitungan kekayaan bersih di Indonesia. Kekayaan bersih bisa bernilai negatif, yakni jika nilai seluruh harta (kekayaan) lebih kecil daripada hutang. Pada Kurva Lorenz, saat ada banyak masyarakat yang memiliki kekayaan bersih negatif maka akan membuat Kurva Lorenz memiliki sumbu vertikal yang negatif (Gambar 3).

Gambar 3. Kurva Lorenz Pembagian Kekayaan di Indonesia, 1993 (kiri), 1997 (tengah), 2000 (kanan)
Pengamatan atas ketiga kurva di Gambar 3 menunjukkan kondisi distribusi yang paling buruk adalah pada tahun 1997 (tengah) dimana Kurva Lorens memiliki posisi paling jauh dari kurva horizontal dan bernilai negatif. Kemudian, kondisi distribusi paling baik adalah pada tahun 2000 (kanan), dimana posisi kurva pada tahun ini paling mendekati garis diagonal.
Dengan perhitungan matematis, Gini Ratio pada tahun 1993 (kiri) adalah 0.897 dan untuk tahun 1997 (tengah) adalah 1,092. Sementara Gini Ratio untuk tahun 2000 adalah 0,690.
(Thomas Soseco)
Artikel Terkait:
- Piramida Distribusi Kekayaan Masyarakat Indonesia
- Skewness dan Kurtosis
- Palma Ratio Indonesia
- Palma Sectors d10+ dan d10++ Indonesia
- Berapa Rata-rata Kekayaan Rumah Tangga di Indonesia?





